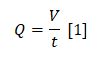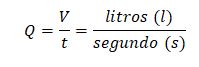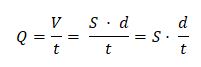Los dos conceptos más importantes que intervienen en el funcionamiento en una instalación hidráulica de riego
El caudal y La presión
Se define caudal como el volumen de agua que atraviesa una superficie en un tiempo determinado.
Si denominamos al caudal Q, al volumen V y al tiempo t, entonces:
Normalmente el volumen se mide en litros y el tiempo en segundos, por tanto el caudal vendría expresado en:
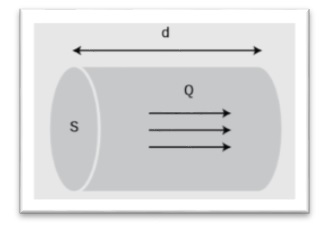
Existe otra expresión para el caudal. Supongamos que estamos midiendo el caudal que pasa por una tubería circular. El volumen de agua que pasará en un determinado tiempo tendrá la forma de un cilindro con una sección igual a la de la tubería (la sección S la medimos en metros cuadrados), y con una longitud d (medida en metros):
El volumen será por tanto equivalente al volumen del cilindro, es decir:
V = S · d
Si ahora vamos a la fórmula [1] y sustituimos tendremos lo siguiente:
Pero aún podemos hacer una sustitución más. Esta ecuación contiene la distancia recorrida por el agua en un tiempo determinado, lo cual no es otra cosa que la velocidad a la cual circula el agua, de modo que podemos escribir:
Donde v es la velocidad de circulación del agua en metros por segundo y S la sección del tubo en metros cuadrado (m2). El caudal por tanto se expresa en: Q = m2 · m/s = m3/s
Por tanto el caudal que circula por el interior de una tubería dependerá del ancho del tubo (sección) y de su velocidad. Cuanta más sección más caudal; a mayor velocidad mayor caudal también.
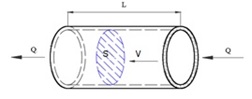
Fig. 1 El caudal que circula por el interior de una tubería depende de la sección del tubo y de la velocidad de circulación del agua. Q = S • v
El caudal se puede expresar en litros por segundo (l/s), litros por minuto (l/min) o bien litros hora (l/h). También se suele utilizar metros cúbicos por hora (m3/h) y metros cúbicos por segundo (m3/s).
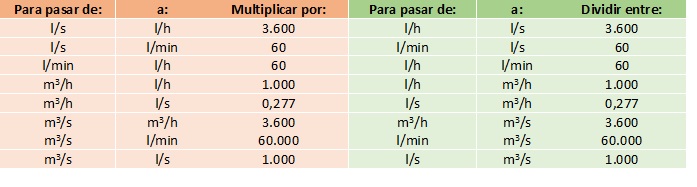
Todas estas unidades se pueden convertir entre sí. Tendremos que emplear las siguientes conversiones para pasar de una unidad a otra:
Tabla I: “Conversión de unidades de caudal”
 Ejemplo 1. ¿Qué caudal circulará por una tubería de 200 milímetros de diámetros si la velocidad del agua es de 1,5 m/s?
Ejemplo 1. ¿Qué caudal circulará por una tubería de 200 milímetros de diámetros si la velocidad del agua es de 1,5 m/s?
La fórmula de cálculo es Q = S · v. Lo primero que debemos conocer es la sección o el área de la tubería. Para calcular la sección utilizaremos la expresión del área de un circulo: S = 3,1416 · radio2. Como el radio es la mitad del diámetro, radio = 200/2 = 100 milímetros; lo pasamos a metros dividiendo entre mil; r= 100/1000 = 0,1 metros. Por tanto S = 3,1416 · 0,12 = 3,1416 · 0,1 · 0,1 = 0,031 m2
Ya podemos aplicar la fórmula; Q = S · v = 0,031 m2 · 1,5 m/s = 0,046 m3/s; para pasarlo por ejemplo litros por minutos utilizamos la tabla I de conversión de unidades de caudal:
Q = 0,046 · 60.000 = 2.760 l/min = 46 l/s
Ejemplo 2. Deseamos saber la velocidad a la que circulará el agua por una tubería de 90 mm de diámetro que transporta un caudal de 15l/s.
De la conocida fórmula Q = S · v despejamos la velocidad. Es decir, v = Q/S
El caudal lo transformamos en m3/s según lo indicado en la tabla I:
15 l/s / 1.000 = 0,015 m3/s
Calculamos ahora la sección del tubo. El radio son 90/2 = 45 mm, que pasados a metros son 0,045 m.
S = 3,1416 · 0,0452 = 3,1416 · 0,045 · 0,045 = 0,0063 m2
Ya podemos calcular la velocidad del agua:
v = Q/S = 0,015 / 0,0063 = 2,4 m/s
b) Presión
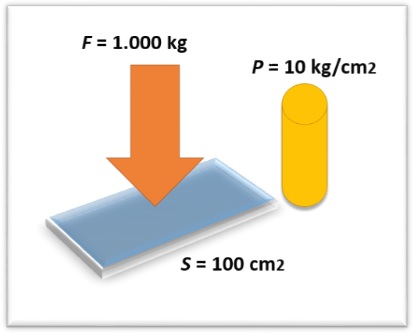
Presión es la fuerza que actúa sobre una superficie determinada. Una misma fuerza puede producir más o menos presión según la superficie sobre la que actúa sea menor o mayor.
Para entenderlo supongamos una fuerza de 1.000 kilogramos que actúa sobre una superficie de 100 centímetros cuadrados. La presión ejercida sobre esa superficie es:
P = F/S = 1.000/100 = 10 kg/cm2
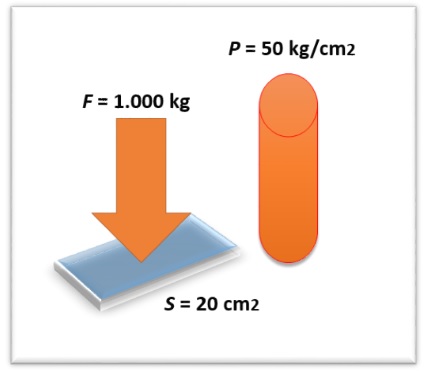
Si esa misma fuerza se aplica sobre una superficie de 20 cm2, entonces la presión ejercida será ahora de:
P = F/S = 1.000/20 = 50 kg/cm2
Por tanto al hablar de presión no es suficiente con indicar la fuerza o el peso, sino que hay que indicar también la superficie sobre la que opera la fuerza o el peso.
Sin embargo, en el lenguaje normal, se abrevia y se habla por ejemplo de 5 “kilos” de presión. Se entiende que estos 5 kilogramos de presión actúan sobre 1 centímetro cuadrado de superficie, por tanto se trata de 5 kg/cm2.
Las unidades de presión más empleadas en hidráulica son:
- atm (atmósfera), Bar, kg/cm2, mca (metros de columna de agua), kPa (kilopascales)
Estas unidades se pueden convertir entre sí ya que:
1 atm = 1 bar = 1 kg/cm2 = 10 mca = 100 kPa
Es decir, para pasar de atmósferas, bar o kg/cm2 a mca hay que multiplicar por 10.
Para pasar de mca a atmósferas, bar o kg/cm2 hay que dividir entre 10.
Ejemplo 3. El manómetro de una estación de filtrado indica 7 mca. Si la limpieza manual hay que realizarla cuando la pérdida de presión sea de 0,6 bar, ¿Es necesario limpiar el filtro?
Vamos a pasar los mca a bar, para ello hay que dividir entre 10. Es decir 7 mca/10 = 0,7 bar. Por tanto hay que realizar la limpieza de filtro pues se ha rebasado la presión mínima.
Para medir la presión se emplean unos dispositivos llamados manómetros. Los manómetros pueden ser de rosca o bien de aguja como se representa en la siguiente figura:
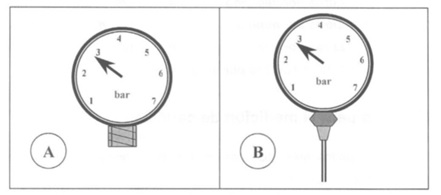
Fig. 2 Manómetro de rosca (A) utilizado para ser instalado en determinados puntos de la red, permaneciendo fijo. Manómetro de aguja (B) utilizado para realizar mediciones puntuales.
Autor: Miguel Ángel Monge Redondo
Ingeniero Técnico Agrícola.
Profesor de Universidad Internacional de Riego.
Si te ha gustado el artículo de nuestro profesor Miguel Angel Monge te invitamos a que visites sus cursos: